
I am a notetaker, and an analog one at that. I always have a notebook at my desk to jot down to-dos, project notes, and other things I need to remember. In an effort to be more eco-conscious, my supply of notebooks is my girls’ old school composition books, which are rarely fully used.
Recently, I grabbed a “new” notebook from the pile next to my desk. Of course, before using it, I had to flip through my daughter’s notes. I had grabbed a science notebook that I’m guessing was from middle school. The large number of graphic organizers, particularly concept maps, jumped out at me. There were concept maps of parts of an ecosystem, a food web, the states of matter, and several other topics.
Noticing that the next book in the pile was a math notebook, I flipped through that, wondering if I would see a similar array of concept maps in there. While the notebook was packed with notes, exercises, and things like place value and conversion tables, there was nothing like what I saw in the science notebook. This got me wondering about the idea of using concept maps in math.
What are concept maps?
The term “concept map” is not new and it’s likely to be, if you’ll pardon the pun, a concept with which you are familiar.
At the simplest level, a concept map is a way to organize information and show relationships visually. While some definitions of concept maps include a wide array of graphic organizers, like Venn diagrams, T charts, and tables, I’d like to focus on a more specific type: those consisting of nodes and connectors. Nodes are where you record concepts or ideas, and connectors (lines, arrows, and/or phrases) show how the nodes and concepts relate.
Concept maps can have either a hierarchical structure or be based around a central organizing theme. Concept maps organized around a central theme are sometimes referred to as mind maps or spider maps. As an example, I’ve reproduced the states of matter concept map from my daughter’s notebook below.
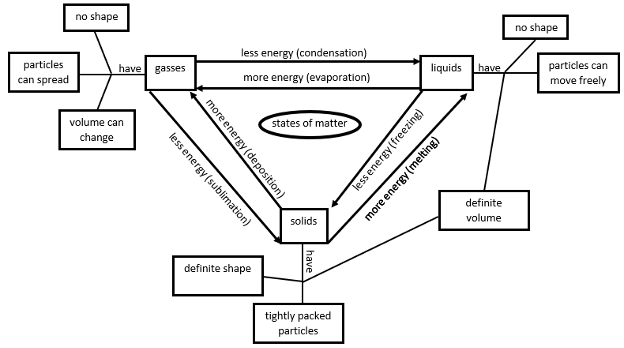
You can also find examples of concept and mind maps at this University of Wollongong website and in this research paper on concept mapping in math. Achieve the Core’s coherence map as well as their graph of the content standards are examples of complex concept maps that you might already be engaging with in your teaching practice.
Concept maps accelerate student learning
You may be familiar with John Hattie’s visible learning project. His original book harnessed over 800 meta-analyses to help determine what factors and strategies research has found to have positively impacted student learning. Over the years, Hattie has continued to add to this body of work, and numerous sites, including Visible Learning and Corwin’s Visible Learning Metax research database, have been created to make this information available to educators.
Searching the Metax database for concept mapping shows that based on 12 meta-analyses of over 1,200 studies involving 26,000 students, concept mapping has the “potential to considerably accelerate” student learning with an effect size of 0.62. For reference, Hattie has defined anything with an effect size of more than 0.4 as having a greater than typical positive impact on student learning.
So what exactly makes concept maps effective? One of the key components of a concept map—the element of connection—taps into a highly effective learning strategy: in “Maximum impact: 3 ways to make the most of supplemental content,” I talked about the importance of creating connections between ideas, particularly new ideas and previously learned ones. Embedding new knowledge into a web of previously learned content frees up working memory, which, in turn, supports deeper learning than rote memorization of facts.
Connecting content, specifically conceptual understanding, is particularly important in math, where conceptual connections help give meaning to processes. The authors of the National Research Council’s book Adding It Up: Helping Children Learn in Mathematics explain that students with conceptual understanding “have organized their knowledge into a coherent whole, which enables them to learn new ideas by connecting those ideas to what they already know.” Creating concept maps in math helps avoid the type of instrumental learning of isolated skills that many of us experienced in our own education, and which my colleague Ted Coe talks about in “We all need mathematical ways of thinking: An ‘out of proportion’ example.”
Connecting content, specifically conceptual understanding, is particularly important in math, where conceptual connections help give meaning to processes.
In his seminal paper on concept maps, researcher Joseph Novak references the distinction between meaningful learning and rote learning. Rote learning is associated with passive acquisition, recognition, and recall of factual content. Meaningful learning is associated with learner-constructed understanding in which new knowledge is integrated into the existing schema of knowledge, resulting in an improved ability to both retain and transfer learning to new settings. A meta-analysis of concept map research showed that the construction of concept maps was associated with increased retention and transfer when compared to reading content, attending lectures, or engaging in class discussions. This effect held true across achievement levels, subjects, and settings and may be attributed to the active engagement required to organize one’s knowledge into a concept map.
Concept maps also pair well with retrieval exercises, which can help students cement their learning. In a previous post about our High Growth for All research project, which recommends ten specific instructional strategies proven to help advance learning, I talked about the idea of retrieval practice. This highly effective practice involves literally retrieving information from memory.
While there are different ways to have students create concept maps, combining concept mapping with retrieval practice, or asking students to create maps based on recalled information rather than information in front of them, can increase the impact of concept mapping. Using concept maps and retrieval practice together is a powerful combination that improves retention of new materials when compared to more traditional ways of studying, like reviewing or rereading the material repeatedly.
Teachers as mapmakers
How can you get started with concept maps in your classroom? A great first step can be doing it yourself.
Concept mapping can help teachers develop a deeper understanding of math and their standards. In her book Knowing and Teaching Elementary Mathematics, Liping Ma examines variations in Chinese and American teachers’ understandings of and approaches to fundamental math topics. In discussing subtraction with regrouping with teachers from both countries, she noticed that the Chinese teachers frequently referred to connections within math topics. These “knowledge packages,” as one teacher called them, represent the teachers’ understanding of math topics not as individual units of knowledge or even as a single progression, but as an interconnected web of concepts. The teacher explained that as you teach a piece of knowledge, “you should know the role of the present knowledge in that package. You have to know that the knowledge you are teaching is supported by which ideas or procedures, so your teaching is going to rely on, reinforce, and elaborate the learning of these ideas.”
There is no one right way to determine the related knowledge for a given topic. Creating even a simple concept map similar to the one shown on page 16 of the book can anchor the current learning in related content, which can help you determine appropriate scaffolds, supports, and enrichment content for your students. It can also give you an idea of what to look for in any student-created concept maps.
Before starting a new unit, consider mapping the unit content beforehand, being sure to include both previously learned content that the new topic connects to as well as where the knowledge is heading, at least at a high level. This can be a great activity for grade-level teams or even cross-grade teams to do together.
Getting started with students
When first introducing concept maps to students, you may wish to build some maps either in small groups or as a whole class so that you can model the process and guide student’s understanding of the mapping. And there is no right or wrong age to get started. Research has indicated that concept maps are a useful tool even with the youngest of students.
While there are plenty of concept map templates available online, I prefer to build a map from scratch to not constrain students. Whiteboards are a great tool for modeling mapping together, and Common Sense Media has compiled a list of concept mapping tools and apps for educators. The Florida Institute for Human and Machine Cognition’s concept mapping tool is free to download, and the “Learn about concept maps” section of their website contains links to documents and videos to help get you started. When working with small groups, the low-tech solution of Post-it notes and chart paper is conducive to rethinking connections and rearranging ideas.
The key to a good concept map is framing the guiding question. You can certainly just ask students to make a map of a particular topic, for example, measurement. However, it can be more effective to provide a question that encourages deeper consideration of the topic, for example, “How can we measure the length of an object?” Simply providing a topic tends to result in a more description-focused map, whereas a well-crafted question promotes more analysis.
Once you have created your question or determined your topic, prompt students to create a list of ideas and concepts related to the question. Novak refers to this as the parking lot. You may want to pre-create a list of concepts. Once students generate their parking lot list, you can either suggest any key terms that they missed or ask prompting questions to elicit them.
The next stage—connecting the ideas from the parking lot and building the maps—can be the most challenging. You want students to develop the ability to make meaningful connections and not just create a linear connection or “string map” like the one Novak shows on page 13 of “The theory underlying concept maps and how to construct and use them.” As students begin arranging concepts, you may need to prompt them to create more specific linking phrases to better articulate what truly connects the various ideas.
In introducing concept maps, aim to emphasize that they are never truly “done.” Students are always gaining new knowledge and understandings of the connections between that knowledge. As such, their concept maps will change and grow, and students should be encouraged to revisit and alter concept maps frequently.
5 times to try concept maps
When you think about using concept maps in math, there are probably a few obvious topics that come to mind, like mapping the types of real numbers and types of quadrilaterals. Those are certainly viable topics. However, concept maps can be used to develop both a deeper and wider interconnection of topics. Like I mentioned earlier, more abstract questions can result in rich maps that connect to multiple concepts.
Let’s look at five specific times to use concept mapping in your math class:
- Unit opener. If you’ve done your own concept mapping for a unit, you know what precursor concepts underlie the upcoming unit. Having students create a concept map related to key foundational skills can help activate their prior learning and provide you with formative assessment data. So, before starting a fourth-grade unit about multiplicative comparison, for example, you might ask students to create a concept map around the question “How do addition and multiplication compare?” You can refer to students’ maps during the unit to help students distinguish between additive and multiplicative thinking.
- Making connections during the unit. As you progress through a unit of study, have students create their own concept maps of what they are learning. At the end of each lesson or lesson series, students can revisit their maps to add new information or new connections. This is also a great way to help students connect what they learn in supplemental time to the whole-class core content. For example, you may have a group of students who are using their supplemental time to review measurement conversion in support of understanding the whole class unit on ratios. At the end of each week, ask these students to consider how they might add what they practiced with unit conversion to their concept map of ratios. Taking beginning and end-of-unit pictures of students’ concept maps can help them see how much their learning has grown.
- Paired activity. Having students work in pairs to create concept maps together can lead to a rich dialogue. As students decide which concepts to add to the parking lot and share their understanding of how the concepts connect, they must both articulate their own thinking and seek to understand their classmates’ ideas.
- Assessing conceptual understanding. Most math assessments focus on checking students’ procedural skill and fluency and their ability to apply these skills to real-world problems. Concept maps can give students a way to demonstrate their understanding of foundational concepts and how they interrelate. In addition to having students create maps from scratch, you can also ask them to fill in partially completed maps or have them correct maps with errors as quick formative checks. Using conceptual maps as assessments moves away from the idea of assessment that represents “closure of a topic, representing to students the closing of a door on a set of skills.” The expansive nature of concept maps gives you a sense of students’ in-the-moment conceptual understanding but reminds both you and them that their knowledge is always growing.
- Year-long map. A wonderful way to close out a unit might be to add to a cumulative, year-long concept map. Ask students to think of the big ideas from the most recent unit. Creating a map that shows connections between big concepts learned across the year can really reinforce the idea of math as a cohesive subject. You can do this either via a map saved on the computer and shared on the white board or on a large piece of craft paper. Students can even add concepts learned in previous years to create a full picture of their math understanding.
Let’s get mapping!
Concept maps are a simple but effective tool for helping students actively organize and consolidate their knowledge. They can be particularly effective in helping them literally see the cohesiveness of math. If you need more help to get started, check out the resources below:
- “Concept mapping” This five-minute BrainPOP video gives a great overview of concept maps and how to create them. It’s perfect for elementary students.
- “Mind mapping and brainstorming apps and websites” This Common Sense Education page includes reviews of 12 mapping apps and websites with information about whether the resource is free and for what grade levels it is appropriate.
- “Learn about concept maps” The Florida Institute for Human and Machine Cognition’s Cmap site contains links to articles about a variety of topics, including focus questions, the importance of linking words, how young children can engage with concept maps, and how to introduce concept maps to students.
- “Mathematics concept maps: Assessing connections” This article from NCTM’s Teaching Children Mathematics journal models how small groups of fourth- and fifth-graders worked through a concept mapping activity.
- “Promoting mathematics connections with concept mapping” This article from NCTM’s Mathematics Teaching in the Middle School journal includes an example rubric for using concept maps for assessment.
- “Using concept maps to link mathematical ideas” This article from NCTM’s Mathematics Teaching in the Middle School journal discusses different ways to use concept maps in middle school.







