
If you are on social media at all, at some point you’ve probably come across a post, or more likely a repost, of someone complaining about “new math” or, rather, the new ways of doing math. These posts range from humorous to vitriolic, but regardless of the tone, they represent a consistent pushback from parents on new approaches to math brought about by the adoption of Common Core and other college-and-career ready standards. The main complaints typically fall into one of several categories: these new ways of doing math are too laborious and make no sense, I have no idea how to help my kid, and what was wrong with the old way of doing things?
Ironically, what may underlie some of this pushback could be the best argument for why we need new approaches to teaching and learning math. I have often wondered about the intersection of those who advocate for teaching math the “old way” and the large proportion of people who are quick to proclaim that they are “not a math person.” This, coupled with studies that show 93% of US adults express some level of math anxiety, would argue that we very much need to learn math differently.
Many of us learned math as a set of rote procedures to memorize and follow without thinking, typically to solve a batch of nearly identical problems. For those of us who struggled either with the initial memorization or with recalling the procedure a month after the test, new ways of thinking about math might help us actually see ourselves as a math person, which research shows all of us are. The goal of current math standards is to help students develop a deep sense of numbers, which supports understanding why various procedures work and gives students a toolkit of multiple ways to approach a task depending upon the specifics of a problem, the numbers involved, and more.
So, what’s new?
Let’s look at some simple examples to show why knowing more than one way to approach a math problem can be more efficient. Say you needed to find how many years there are between 1999 and 1950. Using the standard procedure, you would likely line the numbers up, subtract the ones (9 – 0) and then the tens (9 – 5), moving left until you had subtracted all the place values.
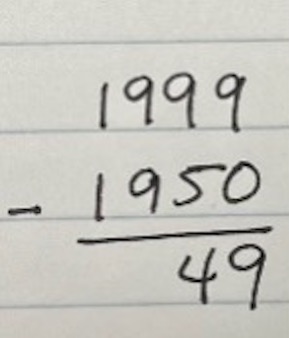
In this example, the math is straightforward. There is no need to decompose a larger unit into a smaller one, that is, you don’t need to regroup or borrow. You can simply subtract each place value.
Now let’s imagine you wanted to find how many years there are between 2024 and 1786. This gets a little more complex if you use the traditional approach. Take a moment to work through the problem the way you were taught. Most likely you lined the numbers up as in the example above and the result looked something like this:
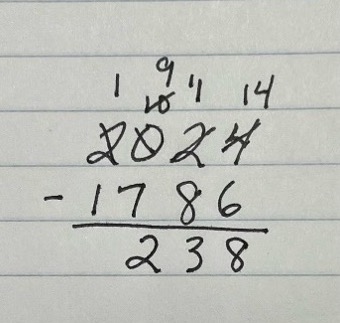
Because the digits in the ones, tens, and hundreds places in the bottom number were greater than the digits in the ones, tens, and hundreds places of the top number, you had to regroup or borrow multiple times, resulting in a lot of crossing out and rewriting of numbers above the original problem.
There is absolutely nothing wrong with the approach; however, many of us were taught it as a process without really understanding the why of it all. When we regrouped the two-thousands place, changing the two into a one and writing a 10 over the hundreds place, what did that mean? Were we really understanding that one thousand is the same as 10 hundreds? A key goal of new ways of teaching math is to have students understand what they are doing when they do use this traditional approach.
More than one way
Even when you understand the approach, the traditional method isn’t the only way, and it may not always the most efficient way to solve a problem, depending upon the numbers involved. Modern standards work toward helping students become fluent with numbers and mathematics. Being fluent means more than getting the correct answer quickly. Fluency is about “thinking about mathematical procedures with efficiency, accuracy, flexibility, and appropriateness.”
So, if we go back to our problem of finding 2024 – 1786, we can see there are approaches that might be more efficient than the traditional approach. For example, you might realize that:
- 1786 is 14 away from 1800
- 1800 is 200 away from 2000
- 2000 is 24 away from 2024
So, to find the difference between 2024 and 1786, you could quickly add 200 + 14 + 24 to get 238.
Frequent use of number lines, a model commonly used in math classrooms now, may allow a student to solve this problem mentally. The three-minute video “What’s wrong with carrying the one?” gives a great explanation of several other ways to solve addition problems once an individual has a strong understanding of numbers. These ideas are not new, and regardless of how you learned, you are likely using some of them without even realizing it. If you had to find the answer to 25 + 39 + 175, for example, would you stack the numbers up and add them like in the example above? You could, but I’m guessing you are more likely to mentally add 25 and 175 to get 200 and then add 39 to that. New approaches to math help students build this type of numerical fluency to make more efficient problem solvers.
Making connections
Understanding the why behind a procedure helps develop what is called relational understanding. Many of us were taught math in a way that promotes instrumental, or disconnected, understanding. For example, we learned about place value and we learned to add and subtract, but we may have never gotten a sense of how they are connected. Relational understanding is designed to help students build a mental web of connected concepts, which supports both understanding and recall. Think of it this way: If you took all the tools from your garage and scattered them around your house, it would be harder to remember where everything was. Instead, we typically organize and store tools according to some sort of schema, for example, a drawer for fasteners, like screws and nails, and an area for painting supplies, like paint stirrers, brushes, cleaners, and primer. Doing so makes it easier to find and use these tools.
Students who can organize and connect knowledge are better at recalling and applying that knowledge. The “new math” standards were consciously designed to incorporate this connection to support relational understanding. In grade 2, for example, students work with arrays (that is, arrangements of rows and columns) as a way to introduce the equal groups concept of multiplication and connect it to repeated addition. They first learn to see three rows of five as 5 + 5 + 5, eventually learning that 5 + 5 + 5 is the same as 3 x 5. Arrays and multiplication also support understanding measurement. In grade 3, students first learn about area by counting squares in an array, ultimately connecting this to the representation of multiplication to realize that they can find the area of a rectangle by multiplying length times width. In grade 5, students connect area to volume. Through concrete exploration they discover that just as three rows of five can be shown as 3 x 5 = 15, four layers of three rows of five can be shown as 3 x 5 x 4 or 15 x 4.
Okay, I get it, but what about the homework?!
While you hopefully have a better understanding of the why behind “new math,” you may still be left with the question of how best to help your child. What do you do when they come to you for help? Where can you go to gain a better understanding of how they are learning math? Here are some ideas:
1. Talk about math regularly
A great way to start is to routinely ask your child either to explain their math homework or to talk about what they did in math class that day. Not only do you learn, but they also gain practice and confidence. Furthermore, the act of sharing with you requires them to retrieve and explain ideas from memory, which is critical to long-term learning. Engaging regularly with your child on math also builds more positive feelings about math. Only talking about math when frustrated creates negative associations with the subject.
2. Be honest
Let your child know that you learned math a different way but are really interested in learning how they do math. Not only will this allow them to be the expert, but it will also model a growth mindset, which helps banish the fallacy that only some people are math people. As they explain their approaches, making connections between their way and your way will also build knowledge for both of you.
3. Embrace the struggle
If you come across a problem that both you and your child are having a hard time with, take a deep breath and remember you are not expected to have all the answers. In fact, even if you do understand the problem, don’t jump in and solve it. What you convey to your child about math, persistence, challenge, and your belief in their ability can impact your child’s feelings about math and, potentially, their achievement. Remind them that struggle is a sign that they are learning; it represents moving from what they know to what they haven’t yet learned but will learn. Tell them that their brain actually grows when they make mistakes learning new material. Try to avoid saying things like “I had a hard time with math, too” or “Math is really tough.” While you may see this as showing empathy, such statements reinforce the idea that math is not for everyone. You can acknowledge the challenge but with a positive spin by saying something like, “Ooh, this looks like an interesting problem. Let’s dig into it!”
4. Prioritize the how
When working through a challenging problem, focus more on the process than the answer. Think of yourself as a coach. Your role isn’t to tell your child how to solve the problem but, rather, to help them move along in the process. A great way to do this is to ask your child questions like these:
- What is this problem about?
- Can you say the problem in your own words?
- What information do you know?
- What are you trying to figure out?
- Where could you start?
- What are some possible ways to solve this problem?
- Can you break the problem into parts?
- Have you worked on other problems that could help you with this one?
- Could you act out the problem with objects?
- Would drawing a picture or a diagram or making a table help you?
- What if you tried guessing the answer? How could you check that your guess was right?
You don’t have to have all the answers
Hopefully you are feeling a little better about supporting your child with “new math.” The next time you start to get frustrated, remember that your openness to learning new approaches models lifelong learning and will go a long way toward building your child’s math skills, confidence, and achievement.
To help you continue learning, here’s a set of resources for developing a deeper conceptual understanding of math and the new ways it is being taught. These are organized from quicker reads and views to deeper dives.
- “9 ‘new math’ problems and methods”org explains commonly used math models to help parents and caregivers gain familiarity and understanding.
- “Parent roadmaps to the Common Core Standards—Mathematics” The Council of the Great City Schools has created resources for each grade from kindergarten through eighth, in both English and Spanish, explaining the key math concepts for each grade.
- Illustrative Mathematics “For families” page Even if your child’s school doesn’t use the Illustrative Mathematics curriculum, you can access short parent resources for each topic in K–5 in English and Spanish on their website. Each explains the key models for each topic.
- GreatSchools math videos These short videos highlight what kind of understanding to look for when students are learning key concepts, from kindergarten through high school.
- Khan Academy This well-known resource can help you quickly learn about a wide array of math skills and concepts.
- Graham Fletchy’s videos Classroom teacher and math specialist Graham Fletchy has created a series of five short videos explaining how the concepts of numbers and counting, addition and subtraction, multiplication, division, and fractions are developed across the math standards. All the videos are less than eight minutes.
- Mathy Matt videos Mathew Felton-Koestler, an associate professor of mathematics teacher education at Ohio University, has created a series of videos explaining different ways to approach different types of problems. His videos span kindergarten through high school and most are less than 10 minutes long.
- Scott Adamson’s videos Scott Adamson is a former high school math teacher, a college professor, and part of the Arizona Mathematics partnership. His videos are longer, typically around 15 minutes, and they focus more on math concepts in grades 5 and up. His explanations of fraction multiplication and division in particular are great for helping demystify these often misunderstood concepts.
- “Learning to think mathematically” This website by The Math Learning Center includes resources about rekenreks, multiplication, the number line, and ratio tables. Although these resources are designed for teachers and are longer, parents and guardians can scan each PDF for the specific models used by their child to get a better understanding of the math behind them.
- “Mathematics resources for parents and guardians” The California Department of Education has assembled a collection of resources to help parents and guardians understand how math is taught today.
- “A family’s guide: Fostering your child’s success in school mathematics” The National Council of Teachers of Mathematics created this 33-page guide covering math from preschool through high school to help parents and guardians understand math standards, approaches to teaching, and ways to support homework and key concepts in math in elementary, middle, and high school.







