The idea of fluency is big in K–12 mathematics education. However, there is not a clear, shared meaning of the word. In fact, if you were to ask educators to define “fluency” in the context of learning mathematics, you would probably get a dozen different answers.
I encourage you to stop reading this post and think about fluency. Go ahead and pause for a moment. This post can wait. What do you believe fluency in math education is?
What fluency is when we’re talking about math?
Sometimes educators think about fluency as getting the right answer quickly. Sometimes, it’s about accurately performing a standard algorithm efficiently or remembering facts. But there is much more to it.
Fluency demands thinking about mathematical procedures with efficiency, accuracy, flexibility, and appropriateness. Being fluent means that students can choose among methods and strategies to solve contextual and mathematical problems, that they understand and are able to explain their approaches, and that they are able to produce accurate answers efficiently.
It helps to also define what I mean by “efficiency,” “accuracy,” “flexibility,” and “appropriateness”:
- “Efficiency” is the ways in which students carry out strategic procedural plans easily, keep track of sub-problems, and make use of intermediate results to solve a problem
- “Accuracy” means students reliably produce the correct answer
- “Flexibility” refers to students knowing more than one approach, being able to choose a viable strategy, and using one method to solve and another method to double-check their work
- “Appropriateness” means students know when to apply a particular procedure
An example: The role of fluency in understanding fractions
Simply memorizing facts and procedures does not a fluent student make. According to research done by the Rational Number Project, students who only memorize will experience challenges in making sense of math. This is especially true when students begin to learn about fractions and operations with fractions. And, even more specifically, difficulty with operations with fractions often stems from a lack of a robust understanding of the idea of a fraction.
For example, children have difficulty internalizing that the symbol for a fraction represents a single entity. When asked if 2/3 is one or two numbers, many children will say that the symbol represents two numbers. When students consider 2/3 as two numbers, then it makes sense that they would try to treat them like whole numbers. For example, when students add two fractions by adding the numerators and then denominators, they are interpreting the symbols as four numbers, not two. Many errors with fractions can be traced to students’ lack of mental images for the quantity a symbol represents.
Students who have not fully developed fluency with fractions often have difficulty ordering fractions, since ordering fractions is more complex than ordering whole numbers. Comparing 1/4 and 1/6, for example, conflicts with children’s whole number ideas. Six is greater than four, but 1/4 is greater than 1/6. With fractions, more can mean less. In contrast, 3/5 is greater than 2/5 because three of the same-size parts are greater than two of the same-size parts. In this case, more implies more.
Being able to order plays an important part in estimating fraction addition and subtraction. Ideally when a student adds 1/4 and 1/3, they should be able to reason, from their mental images of the symbols, that a) the answer is greater than 1/2, but less than one, and b) 2/7 is an unreasonable answer because it is less than 1/2.
Understanding fraction equivalence is not as simple as it may seem. Some children have difficulty noting equivalence from pictures.
Imagine a circle partitioned into fourths with one of those fourths partitioned into three equal parts. Some children may be unable to agree that 3/12 equals 1/4, even though they can see that the two sections of the circle are the same size. Children can struggle to remove the extra lines drawn in the fourth that’s partitioned into three equal parts. But that is just what must be done to understand fraction equivalence from a picture.
All of these challenges related to a foundational understanding of the idea of a fraction can lead to the difficulties children have with fraction addition and subtraction. These difficulties come from asking students to operate on fractions before they have a strong conceptual understanding of these new numbers.
Fluency involves getting answers as well as thinking about reasons, providing explanations, and communicating thinking clearly.
How asking—and answering—“why” can improve mathematical fluency
To help students gain fluency in math, it’s important to help them explore and understand why.
Consider the following problem: 2/3 x 3/4. Most readers will likely be able to compute the correct answer mentally (the answer is 1/2). It is important to be able to get this answer but also to explain how it makes sense. When working with students on a problem like this one, consider asking them questions like these:
- Why does 2/3 x 3/4 equal 1/2?
- Both 2/3 and 3/4 are bigger than 1/2. Why does multiplying produce a number smaller than the two numbers being multiplied?
- Why do we multiply the numerators and the denominators?
Again, both the answer and the explanation of how the answer makes sense are important.
Why does 2/3 x 3/4 equal 1/2? Because when we multiply fractions, we multiply the numerators and the denominators:
- 2/3 x 3/4 = (2 x 3)/(3 x 4)
- 2 x 3 = 6 and 3 x 4 = 12, so (2 x 3)/(3 x 4) = 6/12
- 6/12 = 1/2
Why does multiplying produce a number smaller than the two numbers multiplied? It helps to begin by thinking about the second part of our equation, 3/4, since that’s the larger number.
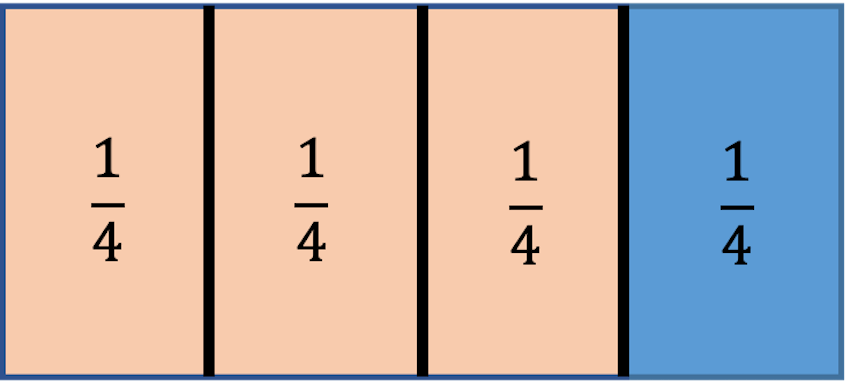
What does 3/4 look like? Picture a rectangle.

To find 3/4 of the whole rectangle, we must cut it up into four equal parts. Each is 1/4.
Now we’re ready to think about 2/3 of the 3/4. If we cut each of the fourths of the rectangle into three equal pieces, we get a rectangle that looks like this.
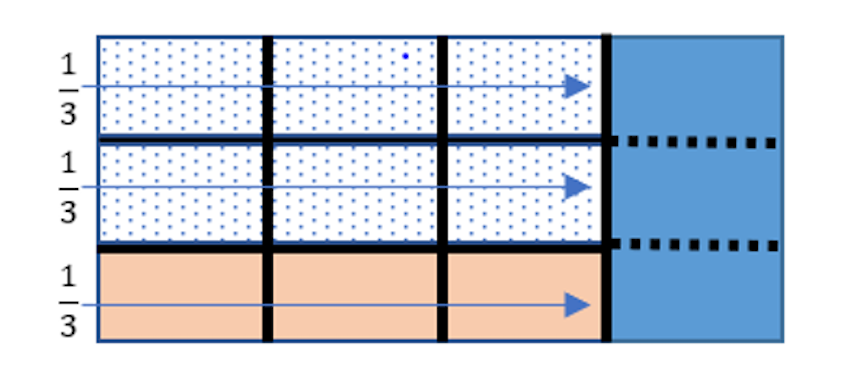
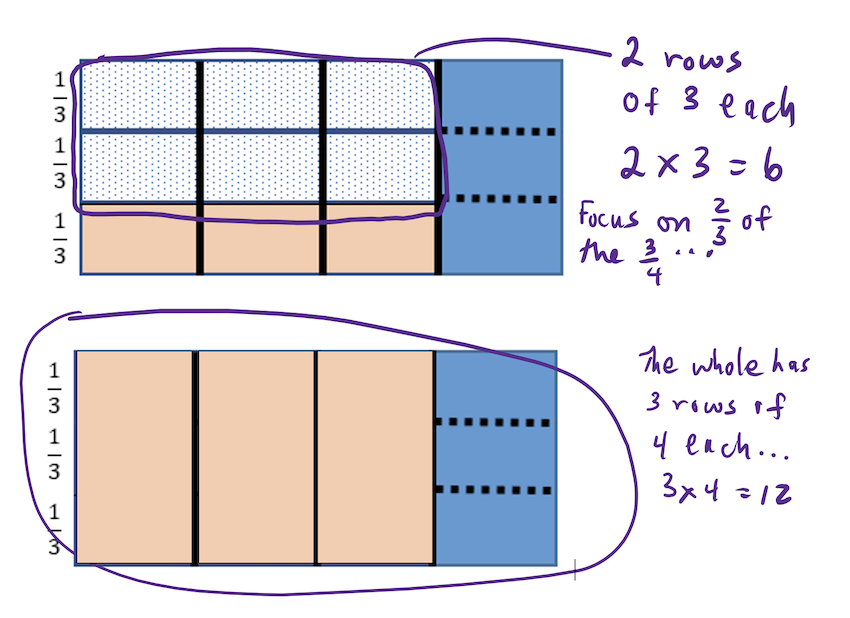
Notice that the white portion of the whole rectangle represents 6/12 of the entire rectangle, or 1/2. Do you see it? That’s why multiplying produces a number smaller than the two numbers multiplied.
Why do we multiply the numerators and the denominators? Look at the diagram again. Do you see where 2/3 and where 3/4 are found?
Worth the effort
Providing reasons for why answers to math problems make sense can be challenging, but it’s critical for helping students move beyond memorization into true fluency in mathematics. How can you explore the why more during your next math lesson?
For even more ideas, I encourage you to read “Engaging mathematical thinking through formative conversation starters” by my colleague Ted Coe and downloading the NWEA conversation starters guides, available for grades 2–8.







