Since leaving the classroom and transitioning into educational publishing, I have primarily worked on math content. This has resulted in me getting tagged as a “math person.” For now, we’ll ignore all the issues of categorizing people as either “math people” or “non-math people” (although you can check out my colleague Fenesha Hubbard’s great article on the impact of such labels). For me, what has come of this labeling is the great surprise expressed by others when I convey my love for and knowledge of children’s literature.
Whether born out of the human need to categorize, or as a result of the prevalence of math anxiety, I have always found it odd that we view the subjects of ELA and math as such polar opposites. The contemporary approach to teaching math—in which students actively test ideas, explore patterns, develop multiple solution approaches, and regularly engage in discussion to both explain their reasoning and hear that of others—shares much DNA with active and engaged ELA classrooms. In my article on helping students develop perseverance in math, I cite ideas from Julie’s “5 reasons to give students feedback on their writing process” to argue that mathematical problem-solving should be treated as a recursive process like writing. I have also explored the benefits of writing in math class—and my experience of being questioned by colleagues about why we would ever ask students to do this.
All this to say, I was thrilled to come across Allison Hintz and Anthony Smith’s book, Mathematizing Children’s Literature: Sparking Connections, Joy, and Wonder Through Read-Alouds and Discussion. The purpose of the book is to help teachers extend the joy of reading aloud to the joy of exploring mathematics, and I couldn’t wait to discuss it with my colleague Julie.
What is mathematizing?
The term “mathematizing” is not new, and you may be surprised to learn that mathematizing is something we all naturally do. Essentially, it is how children (and adults) combine curiosity and mathematics to make sense of the world. When my daughters were young, their grandfather was a giant to them, both in his importance in their life and because he was six feet tall. When considering lengths, they would often think in terms of how many grandpas a given distance would be. They were using a personal frame of reference to make sense of the world in a mathematical way. They were, in essence, mathematizing.
To mathematize is to actively observe, wonder, ask questions, and pose solutions. Engaging in active mathematical inquiry and exploration is exciting! As Catherine Twomey Fosnot and Maarten Dolk put it, “When mathematics is understood as mathematizing one’s world—interpreting, organizing, inquiring about, and constructing meaning with a mathematical lens—it becomes creative and alive.” Mathematizing children’s literature is simply extending students’ natural mathematical curiosity to picture books and stories, encouraging them to make observations, pose questions, and seek solutions based on the story and illustrations.
Mathematizing stories vs. solving a story problem
You may be wondering how mathematizing children’s stories differs from giving students story problems to solve. Although high-quality story problems can be rich and open-ended and also encourage deep and diverse mathematical thinking, many story problems tend to be much more linear and close-ended. Story problems usually come with a set agenda; they are often a way to practice and apply a skill taught in class with little variation or thought required. Even when multiple solution paths are possible, the question being asked is typically very narrow, and it is posed by either the teacher or the curriculum.
In contrast, mathematizing centers around student-generated questions, which may or may not relate to the current topic in math class. Hintz and Smith detail the difference between story problems—where “the problem is defined, and the question is posed”—and exploring math that arises from a story context. With a story problem, “The information to solve is given. The purpose is to calculate and get a correct answer (and probably quickly!), not to think mathematically about the world.” With mathematizing stories, “The power of not posing the question is that children get to be the mathematicians who ask and investigate their own questions.” This transforms students from passive doers of tasks to active investigators of their own wonderings and ideas.
Why mathematize children’s literature?
In illuminating the difference between solving story problems and mathematizing children’s literature, we have begun to unpack some of the benefits of mathematizing. Let’s dig a little deeper into how this approach can support students’ understanding and love of mathematics.
Rediscovering the joy of math
In reading Hintz and Smith’s book, one of the key benefits that struck me was how mathematizing stories makes math—wait for it—playful. I am willing to wager that if you asked people if they thought of math as playful, you might be met with some skepticism. For many of us, math has been taught as a series of facts and procedures to be committed to memory, not as something we would actively seek to explore for the fun of it. Giving children the space and time to explore the world mathematically and allowing them to pursue their own curiosity invites them to enjoy math and to see it as a vehicle for sense making rather than as a chore.
Empowering students to think of math in powerful ways
By expanding math discussions beyond the focus of the current math lesson, mathematizing gives teachers and students a space to explore “Big Ideas” in mathematics. Randall Charles describes “Big Ideas” as ideas “central to the learning of mathematics,” which link “numerous mathematical understandings into a coherent whole.” “Big Ideas make connections,” he adds, and he provides this example of a Big Idea: “Any number, measure, numerical expression, algebraic expression, or equation can be represented in an infinite number of ways that have the same value.” The concepts of place value and of units are other examples.
While different people have identified different sets of Big Ideas (check out our formative conversation starters for one set), exploring Big Ideas helps students understand math as a cohesive, interconnected discipline, rather than a series of seemingly unrelated procedures. For teachers, understanding the connections and progressions of concepts within a Big Idea helps them see where students are in their mathematical understanding and plan instruction not just with the current skill in mind but also with the deeper understanding of how this skill connects to skills already learned, and to still-to-be-learned topics as well.
Expanding the idea of who gets to ask math questions
Typically in math classes, it is the teacher or the curriculum who pose the questions. While students may ask questions of each other in discussions of different solution methods, this is different from posing mathematical questions.
Allowing students to ask mathematical questions about observations from books accomplishes several things. First, you are helping them see how mathematics can be a means for understanding the world. By guiding them through asking questions and exploring ways to understand them mathematically, you help them learn that real math exists beyond a textbook page. Such opportunities reinforce students’ view of themselves as mathematicians capable of wrestling with big, open-ended, and even messy mathematical ideas. Finally, the problem-posing that comes out of mathematizing literature can support deeper learning and enjoyment of math. A meta-analysis of 20 research studies on problem-posing showed a “significant impact on learners’ problem-solving skills, mathematics achievement, level of problems posed, and attitudes towards mathematics.”
Hearing children’s thinking and listening to understand their reasoning
Encouraging rich dialogue is a key element of a math classroom. What is unique about the dialogue that happens when exploring math concepts this way is the breadth and depth of concepts explored. Because these discussions are not restricted to the math topic of the day, you can get a broader sense of students’ mathematical understanding relative to a variety of concepts.
_____________________________________________________________________________________
How can you mathematize?
When Mary first introduced mathematizing to me, the potential for this kind of expansive thinking naturally led me to the question: How do I get started? Fortunately, mathematizing children’s literature won’t require you to build a whole new classroom library (which was my initial concern). It begins with looking at the books you already have—through a new “mathematizing” lens.
Hintz and Smith suggest taking the following three steps to begin your mathematizing journey.
1. Choose texts
Start by exploring which books in your current library fit into the three mathematizing categories: text-dependent books, idea-enriching books, and illustration-exploring books. This is a great way to sharpen your lens and uncover hidden potential in beloved titles. Keep in mind that many books naturally overlap categories, so there may not be a perfect fit. When choosing books, the single most important factor to consider is whether it sparks interest.
Text-dependent books might be thought of as “mathy” books because math is central to the story’s plot. These books invite readers to think like mathematicians and are hard to grasp without applying math skills. Some are simple counting books or stories that explore division, multiplication, and fractions through sharing. Others focus on more advanced concepts like area, perimeter, spatial reasoning, or even geometry. A personal favorite is Sir Cumference and the First Round Table.
Idea-enriching books have lots of potential, but mathematics is not central to the story. In these books, pausing to notice math ideas can deepen understanding of the setting, characters, plot, and themes. These kinds of books work particularly well with the “Open, notice, and wonder” exercise featured later in this article. Listening to students’ noticings and wonderings during a read-aloud reveals how mathematical thinking can sometimes unlock a story’s deeper meaning. For example, Hintz and Smith detail how trying to determine the height of the diving board in Jabari Jumps gives insight into Jabari’s character: he is brave to jump from so high up!
Illustration-exploring books offer brief moments where you might pause and think mathematically. For example, the illustrations might provide opportunities for counting, or they may show different combinations of the same number of animals, friends, or balloons. Sometimes, illustrations alone can spark fresh insights about the story, math, or both.
Being open to what students notice and wonder, and encouraging them to approach books with curiosity, can reveal mathematical concepts in ways that aren’t obvious to us as adult readers. When exploring Lizi Boyd’s wordless book Flashlight, students might initially focus on the nature revealed in the flashlight beam. With further exploration and an invitation to mathematize, they may also begin thinking about the fractions and angles represented by the beam of light, or even what fraction of the child is illuminated when the light is turned on them.
2. Explore texts
Once you’ve chosen a text, you can explore it through multiple reads, uncovering new ideas and connections each time. A good example is The Mitten by Jan Brett. This picture book is based on a traditional Ukrainian folktale and works nicely as a K–1 read-aloud. It tells the story of a boy named Nicki who loses one of his white wool mittens in the snow. As forest animals crawl inside for warmth, the mitten stretches beyond what seems possible to make room for each new guest, inviting readers to think about size, space, and the story in playful and meaningful ways.
Mary and I decided to do multiple reads of The Mitten together, to explore how we might approach this with a class.
“Open, notice, and wonder” exercise. We began with an “Open, notice, and wonder” read of The Mitten. This approach helped us slow down and listen closely to what students might genuinely observe and question as the story unfolds. Here’s our running list of ideas that came up during the read-aloud, shared in the kinds of words young learners might use.
- I see the house and the clothes they wear. It looks like the story happened a long time ago in a different place.
- There are so many yarn balls in the house!
- How much yarn do you need to make a mitten?
- It looks super cold where they live. The fire looks cozy, and the snow is really deep.
- How big is a mole?
- The mitten was just the right size for two animals.
- How many animals can fit inside the mitten?
- The animals look cold, even though they have fur.
- I wonder how stretchy the yarn is.
- They let new animals in because they’re afraid of their claws and teeth. Would some animals eat the others?
- The animals want to be warm more than they’re scared of each other.
- Could Nicki fit inside the mitten, too?
- How much bigger can the mitten get?
- What does “make room” mean? Can the mitten keep stretching forever?
- How many animals are in the mitten now? Is the mouse in there, too?
- What is Nicki thinking when he sees he’s missing a mitten?
- How did something so tiny, like a mouse or a sneeze, make the mitten pop?
- Nicki looks really happy when he finds his mitten!
Focused reads. After building our notice and wonder list, we revisited it to find opportunities for deeper exploration. We looked for moments where students’ observations could guide focused reads—whether centered on the story, the math, or both. We also noticed a few places where science concepts could naturally be introduced. Below is a summary of concepts to consider for focused reads. The starred concepts are the ones we would choose to explore next.
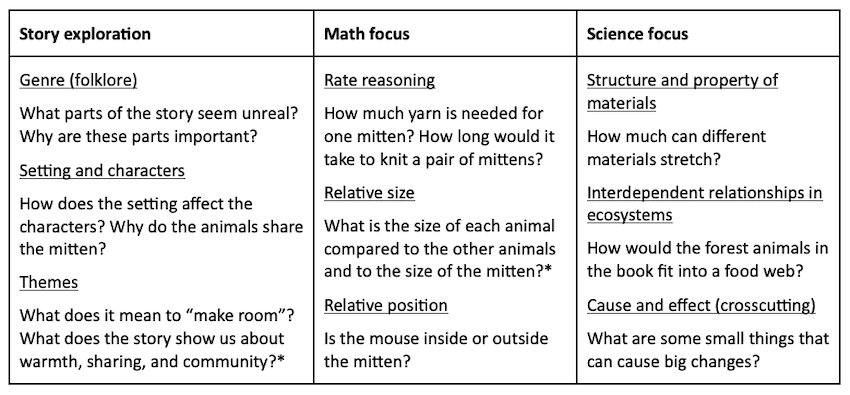
3. Extend texts
The final step in mathematizing children’s literature is generating meaningful real-world problems and tasks based on students’ noticings and wonderings.
Story extension. A powerful way to extend The Mitten is by connecting the story to students’ personal lives and communities. One natural entry point is the theme of sharing. You might begin by asking students some of the following questions:
- Can you think of a time when you shared something? What did you share, and how did it make you feel?
- Have you ever shared something even when you didn’t want to? What happened, and what did you learn?
- What are some ways you see people sharing at school, at home, and in your neighborhood? Why do people share? Why is sharing important? How could people be better at it?
Based on students’ responses and interests, the class could create a mural about sharing. The mural might show different places where sharing happens and include students’ ideas about why sharing is important and how we can all get better at it.
Math extension. Relative size is a great concept to explore with this book, as each succeeding animal that enters the mitten is larger than the previous animal. And, of course, the mitten itself grows with each new animal. In exploring ideas related to size, students may wrestle with the following mathematical concepts:
- Measurement attributes. Students might think about different ways to define and compare the size of the animals: length, height, weight, or how much room they take up.
- Units. Much like Mary’s daughters’ thought of length relative to their grandfather’s height, students may consider the size of the animals relative to one of the other animals. For example, how many mice or moles equals a bear? Children may ponder which animal would make the most sense to use—a smaller animal or a larger one—and the relative merits of each approach.
- Capacity. Students may explore ways to compare the original size of the mitten to the size after the bear enters it, and perhaps to the size of it at the very end when Nicki’s Baba stares at the two differently sized mittens in wonder. Students might also be curious about the size a mitten would need to be to actually fit a bear.
Depending upon which idea students choose to pursue, you can provide them with various tools (paper, pencil, yarn or string, scissors, rulers) to begin exploring relative size. “The Mitten measurement task” shows how a kindergarten class explored the idea of how big an actual mitten would need to be to fit all the animals in the book.
Go out and mathematize!
We hope this article has inspired you to try mathematizing in your own classroom. To get a fuller sense of the process and the reward, we encourage you to check out Mathematizing Children’s Literature. In addition to providing a deeper explanation of the benefits of mathematizing literature, the book gives many examples of specific books and the types of noticings and mathematical explorations they might spark. It also includes templates that can guide you through different types of reads and help you spark, amplify, and deepen your students’ mathematical curiosity.
