Education leaders, politicians, researchers, and teachers have been attempting to define proficiency in mathematics for years. Within the current educational system, the most popular measure of a student’s ability in the discipline of mathematics boils down to a single score on a single test administered once a year. That is not enough.
The current landscape
Though standardized testing has been a part of education for many years, No Child Left Behind really made the push to reduce student achievement to a single cut score and label students as “below,” “approaching,” “on-level,” or “above.” This has had a ripple effect on nearly every aspect of education, from the perceptions of the student and their opportunities to teacher evaluations and district-level funding.
But the impacts go beyond that to define not only what math should be taught but how it should be delivered. High-stakes assessments place an overemphasis on product over process and memory over cognition. To meet the demands of the standardized tests, narrowed learning progressions are designed to teach content as quickly as possible so students have a fair run at the test each year. This reduces mathematics to a rigid timeline of skills and shortcuts, rather than a rich landscape of concepts that develop and connect to each other organically. Because most classrooms are forced to rush down the prescribed track, computational speed and accuracy become the primary measure of a student’s success—and are often mistakenly equated with proficiency. All this rushing to perform also keeps teachers from opportunities to make genuine connections to the big ideas, transition naturally between concepts, or teach flexibly without regard to the traditional sequence.
An alternate model for assessing proficiency
Standardized testing isn’t going away, so the best place to start the search for a better approach is with redefining what it means to be proficient. What if the true measure of a student’s proficiency in mathematics was more natural, authentic, and comprehensive?
In Adding It Up: Helping Children Learn Mathematics, Jeremy Kilpatrick, Jane Swafford, and Bradford Findell propose a five-strand measure of successful learning in mathematics. The five interdependent strands of proficiency are:
- Conceptual understanding: The ability to comprehend the ideas and relationships behind the procedures
- Procedural fluency: The ability to carry out math procedures accurately, efficiently, and flexibly
- Strategic competence: The ability to solve unfamiliar problems by choosing the right strategies and tools
- Adaptive reasoning: The ability to think logically, justify a solution or approach, and reason through presented information
- Productive disposition: The ability to see math as useful and see oneself as capable of doing mathematics
How much more powerfully could a student’s achievement in mathematics be described using these five strands? Imagine what a teacher could do with such nuanced understandings about a student, as opposed to what they can do with a single percentage of multiple-choice questions answered correctly. Breaking a student’s math journey into five categories allows for richer feedback on strengths and areas of growth.
Student examples
Consider a student who has been labeled “above grade level” in math on the past three years of standardized assessments. Perhaps this student is truly accurate and efficient in their calculations with all four operations (that is, procedural fluency) but sometimes has difficulty with transferring a concept to another unfamiliar context (adaptive reasoning) or understanding why the procedure they have memorized and can quickly reproduce actually works (conceptual understanding). This is, in fact, the story of many “advanced” students in elementary school. Though computationally fluent, many have difficulty explaining their reasoning, connecting ideas, or representing thinking in multiple ways, all skills not measured by standardized tests. Without multiple measures of proficiency, this oversimplified view of “above grade level” stunts the student’s opportunities to grow in other areas and gives parents and even peers a false sense of what success in mathematics looks like.
Now consider a student who has been labeled “below grade level” for the past three years. Since intervention opportunities have been provided based on this test result, the student has spent significantly more time than the “above grade level” student on building concrete and pictorial models to develop their understanding of how the math works. This has resulted in a stronger ability to choose the right strategy and tool for a situation (strategic competence). But if we rely solely on a test focused on procedural fluency, this student’s growth in other areas—and eventual gains in fluency—may go unnoticed.
We are doing a disservice to both of these students when we expect a single measure of their ability to dictate their entire capacity for finding success in the discipline. Therefore, our mindset about how to assess students and report on these aspects of proficiency in mathematics needs to change.
Sample tasks for assessing the five strands
High quality assessment consists of providing a balance of formal and informal opportunities to show understanding. Rather than retrofitting one of the strands into an already existing assessment, I encourage you to design new assessment tasks that target a specific strand.
Below are a few sample strong tasks that can measure proficiency or growth, depending on the assessment’s purpose and timing. In presenting and categorizing the tasks in the ways I have, I also hope to illuminate some defining traits of strong assessment practices:
- There is no single, expected path to solve any of these problems.
- No task is designed with a “quick” answer as the measure of proficiency; in some tasks, there isn’t even a single correct answer. In all cases, the student’s line of thinking, their approaches to the problem, their representations of the problem, their strategies chosen, and the justification of their answer are all more powerful measures of proficiency than the correct answer.
- All tasks touch on a concept familiar to students but likely present a context or situation that may be unfamiliar or new. Encouraging students to show their abilities in a novel scenario highlights their ability to apply mathematics to a variety of situations, which is an underlying goal for each strand as well.
For more great assessment task ideas, try out Open Middle problems, our free Formative Conversation Starters, or even student discourse as formative assessment.
Conceptual understanding
Task: Given the number 3/8 on the open number line as shown, locate the number 4/3.
This task assesses a student’s ability to use spatial reasoning to accurately place a number on the number line relative to another. Students must understand the relationship between 3/8 and 1 whole (both conceptually and visually) before they can use the relationship between 1 and 4/3 to plot that point. Student performance on this task will reveal misunderstandings or validate student capability in grappling with the concepts of magnitude and division of a whole into equal parts.
Procedural fluency
Task: Place the numbers 0–9 exactly once into the spaces in the expressions below such that each expression has a value of 32.
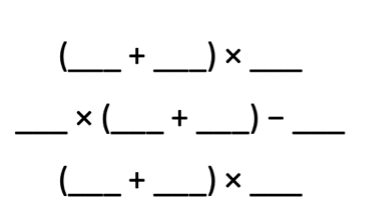This task assesses a student’s ability to efficiently and accurately evaluate expressions step-by-step using the order of operations in a creative way. While many traditional assessment items can measure a student’s ability to follow a procedure and compute an answer accurately, creating a more rigorous task such as this reveals more about how the student applies known processes or approaches to an unfamiliar situation. How the student begins this task can be just as telling, if not more, than their ability to create three accurate expressions.
Strategic competence
Task: A class is building a rectangular garden. They only have 72 feet of fencing to go around the garden. What dimensions of the garden would guarantee the most area for planting?
This task assesses a student’s ability to formulate, represent, and solve a mathematical problem. No matter the solving strategy, the student should be encouraged to model the relationship in some way and rely on geometric and algebraic reasoning to come to an authentic conclusion.
Adaptive reasoning
Task: A woman runs two races of equal length. In the second race, she finishes in 80% of the time it took her in the first. Does this mean she ran 20% faster? Explain.
This task assesses a student’s ability to analyze a proportional relationship and deeply consider the actual difference between a 20% reduction in time and a 20% increase in speed, though these are sometimes incorrectly interpreted as the same thing.
Productive disposition
Task: Design a math game for younger students that helps them learn about multiplication. What kind of game would you create? What is most important in the experience younger students have with your game and why?
This task assesses a student’s ability to think creatively about what aspects of mathematics would be important to convey to younger students. They will, in turn, project their own values in learning mathematics and show confidence in their own ability to learn and use math.
When to apply the data from five-strand assessments
Though I’ve spent a considerable number of words criticizing the improper application of standardized test results in this article, I believe they are still a viable metric as long as they are a) applied to a holistic understanding of the student in the right ways and b) used as one of many data points that tell a more comprehensive story of a student’s learning trajectory. In fact, this is how we recommend schools testing with MAP® Growth™ use the assessment’s data.
Collecting data year-round from multiple perspectives strengthens teaching and aligns understanding among teachers, parents and other caregivers, and students. Here are some great times to apply the data.
When planning instruction
Knowing specifically what to reinforce and build from with each student is a powerful tool. Labeling students as “below” or “above” or “good at fifth-grade math” doesn’t inform how to push them to develop multiple dimensions of proficiency.
For more ideas on how to use MAP Growth and other assessment data when planning instruction, visit our archive of posts on using assessment data here on Teach. Learn. Grow.
When making decisions about student grouping
Groups based solely on a single assessment score won’t be as effective as those established from purposefully grouping students based on their strengths. Basing groups on multiple perspectives increases flexibility of grouping, ensuring that groups don’t inadvertently become ability tracks. For example, perhaps you want to group together your strongest “conceptual understanding” students to make a short presentation for the rest of the class connecting your current unit to content they’ve already learned. Or perhaps you decide to mix the groups so everyone in the class can benefit from having someone nearby who can explain the big idea behind the content you are currently exploring.
When communicating with parents and guardians
A student’s achievement in each of the five strands is great information for parents and other caregivers to have and can help structure conferences or answer the age-old question “What can we work on with them at home?”
During student self-assessments
Five-strand data isn’t powerful for just you or family members; let every student in on your insights, too. For example, if you are about to enter a division unit and a student knows they could use more practice representing their thinking, encourage them to self-advocate for more opportunities to practice with concrete and pictorial models. Additionally, students who may not be proficient based on a standardized test measurement can better see and define their strengths and possibilities for growth.
When framing the “above grade level” conversation
Having more data to support a decision to put a student on an advanced math track never hurts. But being able to clearly show parents and other caregivers where there are still areas of growth for a student is vital. Being computationally “fast” in math class isn’t the same as being 100% ready to tackle higher-level mathematics.
The ultimate goal
We, as members of the current educational system, should put forth a concerted effort to create a new multi-dimensional model of proficiency in mathematics. A single data point can’t define one’s achievement in mathematics. By expanding to five strands of measuring success, we commit to redefining what being “good at math” looks like and can find more opportunities to let all students show their mathematical prowess.
