Think back to a time in your schooling when you saved studying for the last minute. Perhaps by accident or perfectly on purpose, you chose to wait until the night before an exam to cram the material. After you took the test, how well could you remember the content? How well can you remember it now?
Research on memory in the last 50 years has helped us identify the most effective strategies for learning, remembering, and applying information. This research can explain why those tests you crammed for in high school by studying the same type of problem repeatedly until you showed proficiency led to you forgetting that concept by the time the year was over, if not sooner.
There’s been a lot of buzz lately around the idea of spiral review in mathematics. With spiral review, teachers revisit previously learned content throughout the school year to improve students’ retention. But which aspects of this teaching strategy hold weight in how our brains remember? What does research say about spiral review?
What we know about memory
How we remember (and how we forget) has been studied by scientists for hundreds of years. Many theories have been developed about how we can best commit information to memory and continue remembering it for years to come. But here are some of the basics:
- Memory must be reconstructed, rather than reproduced, but reconstruction is prone to error.
- The timing and duration of our exposure to content affect our ability to remember.
- Forgetting is an unavoidable—yet vital—component of learning.
Beyond that, many theories have been developed about the aspects of which memory consists. For example, Piotr Wozniak theorized in 1988 that there are two components of memory: stability (how long an idea can last in memory before being forgotten) and retrievability (how easily an idea can be retrieved from memory).
Though often conflated, these two concepts give us a good idea of how our brain works when storing information. Depending on the stability of the idea, we may be able to remember it for longer before needing to review it again. After reviewing it, we have an easier time retrieving it in subsequent events, and we strengthen its stability (that is, more time can go by before we must review it again to keep remembering). Wozniak’s theory is the foundation of spiral review in mathematics.
The fragmented nature of learning
Our educational system is confined by the expectations and schedules in which learning must take place. A set of academic standards is broken down into pieces to be tackled one by one throughout the year. But a whole is not always achieved simply by the sum of its parts, especially in the case of learning.
If students learn to tackle a particular skill outside of the broader context of the discipline and by practicing only that skill repeatedly in isolation before being tested on it, they often fail to activate authentic problem-solving and decision-making abilities. This technique of teaching and practicing concepts one at a time, sequentially, and in isolation from other concepts is called blocked practice. When students taught only blocked practice in math class are faced with a summative assessment that combines the entire range of skills they’ve learned individually, they struggle to discern which skill is needed and when.
Further compacting this issue is the fact that review of prior content in the classroom takes a back seat to the pressure of continuing forward into the new content that must be covered in one year’s time. Students feel this pressure and may succumb to the strategy of cramming, or massed practice, I mentioned earlier.
Blocked and massed practice are two of the least effective methods for committing information to memory, yet most of our math textbooks remain focused on this format of teaching and learning. By making small changes to how your students acquire and practice new learning in your classroom, you can put years of research in brain science to good use.
Unlocking student potential with spiral review
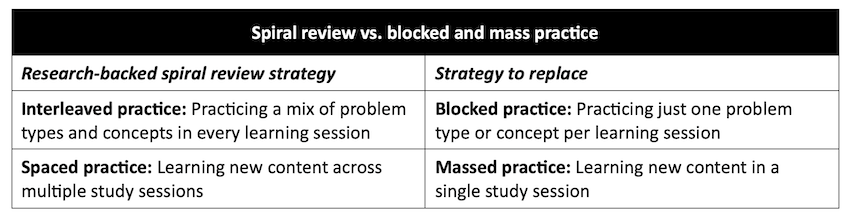
We know what isn’t working in maximizing retention of learned content, but what does research suggest can work? Spiral review. The techniques that can maximize the retention of content and form the backbone of effective spiral review in mathematics are interleaved practice and spaced practice.
Interleaved practice is the intentional habit of mixing types of problems and learned concepts within a single practice session. Rather than asking students to complete a single problem type or strategy repeatedly with blocked practice, this technique gives the brain time and space to position each new topic of learning within the connected framework of knowledge it has already constructed about the discipline.
Spaced practice is the opposite of massed practice. It is the intentional habit of spreading out the time invested in a learning opportunity over multiple sessions to improve understanding and retention. Rather than focusing on the new learning in a single block of time, this technique allows the brain time and space to reconstruct meaning over several learning sessions, which can strengthen the recall of the content.
Spiral review strengthens the stability and retrievability of ideas students acquire during learning, but the benefits of this approach stretch far beyond simply remembering.
Interleaved and spaced practice reduce the cognitive load of new learning. Instead of forcing learners to grapple with the entirety of an idea at once, before practicing it repeatedly, spiral review helps students digest new learning in smaller sessions that can be spaced out to support better understanding and keep the new learning from feeling overwhelming.
Interleaved and spaced practice also naturally force connectedness of ideas within a discipline, making spiral review in mathematics especially worthwhile. Instead of seeing a year of math standards as a list of skills to be checked off, teachers can continually force students to contend with how the new learning is pieced together within the framework built by prior learning. Since students must complete mixed problems across sessions that are spaced out, they spend a lot of time analyzing a variety of situations and choosing a strategy to solve. This is an authentic way to practice transferring skills they know to new contexts so that when those new contexts arrive (like during a summative assessment, for example), they have plenty of strategies at their disposal.
Let’s dive a little deeper into each of the two research-backed strategies that make up spiral review, starting with interleaved practice.
Interleaved practice and its impact on mastery
Interleaved practice can be far more difficult to put into effect than spaced practice because it can feel counterintuitive to learners. In fact, the common phrase “Practice makes perfect” is often used to describe what many people believe is the best way to get better at something: intentional, repeated practice. In one of the earliest studies on interleaved practice, however, participants guessed that repeating the same task over and over was the more effective strategy of the two in their own memory performance; defying popular belief, the data from that same study showed that interleaved practice was unanimously superior to blocked practice.
Research shows that blocked practice creates an illusion of mastery. Students acquire knowledge on one topic and are then tested on just that topic, repeating the exact same strategy numerous times before moving to the next math topic. Because most of their time is spent working with just one strategy at a time, students appear to be doing well when assessed. But with blocked practice, students don’t have practice recognizing the type of problem or strategy out of context, which is often the most difficult part of mathematics for students.
Interleaved practice is an acquired taste; in the moment, students will feel less successful, much like growing pains. In fact, research suggests that a student’s accuracy during an interleaved practice session will most likely be lower than in a blocked practice session, which can be demotivating. But when students arrive at a summative test that combines many concepts they’ve learned, the average accuracy of students who had used interleaved practice could be as much as double that of the students who used blocked practice to prepare for the test. The difficulty in the short term leads to better recall and application of learning in the long term—the goal of spiral review in mathematics in the first place.
Tips for incorporating interleaved practice in your classroom
Interleaved practice can feel tricky to execute because of the mental shift it takes to embrace the method. But there are a few small things you can do:
- Start small. Instead of mixing an entire series of practice problems in every lesson, start by offering just a few mixed practice problems and building from there.
- Lean into the discomfort. Help students understand that it’s okay if they are initially less successful with interleaved practice since the strategy to solve problems will no longer be predictable and repeated.
- Keep an eye on the goal. Share the exact reasoning behind interleaved practice with students and help them commit to the hard work of choosing a strategy on every problem because it will benefit them in the long run.
Spaced practice and its role in learning
Ever wonder why a tool like Duolingo is so successful for learning and remembering a new language? Among other techniques, spaced practice in Duolingo is used to help you consume the new learning in pieces over time so that your brain has more opportunities to solidify connections between ideas and consolidate your long-term retention. Research shows that with the exact same amount of time devoted to either several spaced practice sessions or one massed practice session, student performance is higher using spaced practice.
As you can imagine, there’s no magic formula for the exact amount of time between exposures to new learning, because every brain and idea needing to be remembered are a little different. This is why developing a universal model for spiral review in mathematics continues to be challenging.
Traditional models of spaced practice can produce some improvement in long-term memory retention. The Leitner System, developed in 1972, relies on spacing out content written on flashcards based on whether a student can remember it following a given time interval. The SuperMemo Method, developed and distributed via computer by 1994, relies on an evaluation of the difficulty of each piece of information to determine the best time interval between exposures. These systems developed the backbone for many memory applications today that use flashcards as a memory tool (e.g., Quizlet) as well as advancing our understanding of how memory works.
Tips for incorporating spaced practice in your classroom
Many class curriculums try to simulate a one-size-fits-all spacing of content, but a system of spaced practice that is personalized and adaptive is most effective for maximum long-term retention. Time is not the only factor in these models. The personalization must consider the complexity of the content, the learning styles of the student, the time between exposures, the connections to other ideas in the discipline, and more.
This may seem impossible to do effectively in a classroom of diverse learners, especially if the curriculum you use supports a massed practice model of memory storage. But there are a few things you can do:
- Leverage your warm-ups. This short part of your day has the potential to reinforce learning for vast amounts of content from past learning experiences.
- Activate prior knowledge. This can serve two purposes: memory retrieval for past concepts and preparation for new concepts.
- Practice old and new concepts together. Though your curriculum may focus on practice content from the current lesson, find ways to insert practice on older content as well.
- Find the content that gets the least love. While practicing addition in math class or finding the main idea in ELA class may naturally occur often, try to find the concepts that get reviewed less often and bring those into the spotlight routinely.
- Advocate for adaptive practice software. Talk to your school or district about computer programs that are built on spaced practice science and can do the personalization, timing, and data gathering for you.
Learn more
For more ideas on strategies that can support learning in your classroom, read about our professional learning offerings for math educators and browse the archive of math posts here on Teach. Learn. Grow.
